From the Surface to Space – Watts Up With That?

Kevin Kilty

In my effort to produce the series called “Earth’s Energy Imbalance, parts 1-3” I left open a couple of ideas that simply became loose threads for another time. That time has arrived, partially because of a recent publication that caught my attention.

Background

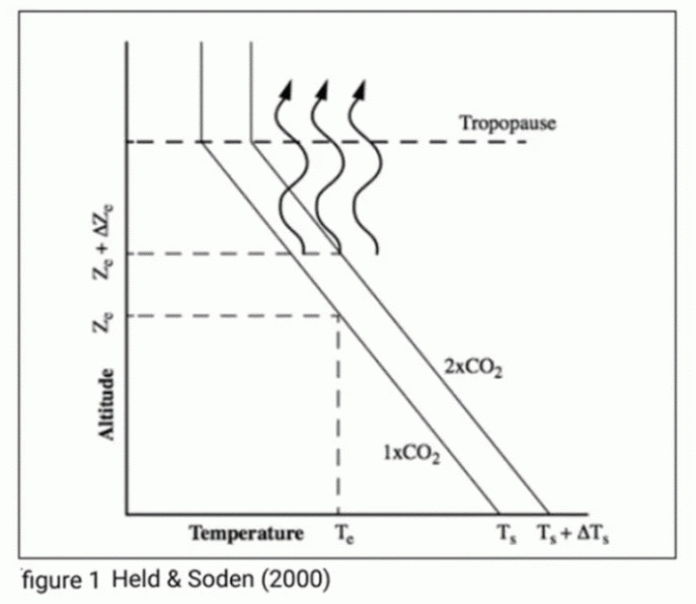
As summarized in Earth’s Energy Imbalance part II the theory of response to radiative forcing from CO2 is most simply explained using an idealized, 1-D atmospheric profile. This explanation is shown in Figure 1, and for purposes of background its explanation is this:

With a fixed Te and fixed gradient (Lapse rate Γ)  surface temperature then becomes; Ts = Te + ΓZe. In this simple model only changes in Ze matter. Now the argument takes the following path.

An increased concentration of CO2 in the atmosphere makes the atmosphere more opaque to outgoing infrared radiation from the surface. Thus, to have a CO2-doubled atmosphere equally transparent above Ze to enable escape of the average photon, Ze must reside higher in the atmosphere. A doubling of CO2 makes the more opaque atmosphere equally transparent above at Ze+150m. However, the invariant gradient of 6.5K/km means the temperature at Ze+150m is lower by about 1K, and according to the Stefan-Boltzmann law this amounts to a reduction in outgoing radiation by about 4W/m² (236.3 = σ 254⁴). There is an energy imbalance that warms the entire atmosphere and surface.

This is an analysis dependent entirely on a temperature profile with an invariant temperature gradient. Let me just say as an aside, that sometimes a very simple and valid explanation is pertinent to an imagined problem; but the imagined problem is different than the problem of pertinence. I think we are facing such a situation here.

Nonetheless, elements of this same 1-D thinking are pervasive in the climate debate.[1]  I don’t want to speak for Dr. Spencer, and perhaps he’d elaborate on this topic, but in a comment I made in “Earth’s Energy Imbalance, part II an Addendum” I mentioned something he’d written on a listserve elsewhere:

“…Roy Spencer has said that when it comes to climate change, the problem doesn’t realy [sic] involve “weather” but is largely a matter of radiative transport surface to space, which is why 1-d models work about as well as global climate models. I agree, but only to a point. I think convection, and advection from tropics to poles are also important, but not even included on the list of feedbacks. Lindzen has lately been emphasizing that poleward transport processes are very important. The whole question is so complicated that it is bound to generate strong disagreement ….”

Because of the focus on 1-D geometry, an important question to explore is “What does an atmospheric profile, a 1-D column, tell us about heat transport surface to space?”

The short answer is that it tells us nothing definitive until it is augmented with other information. The reason for this is that any number of processes can arrive at the same atmospheric profile. The forward problem, going from processes to profile, arrives at a unique answer. The inverse problem, going from an observed profile back to the processes producing it is not unique, but rather infinitely degenerate. This is the same problem I identified as fatal to a published paper arguing for CO2 having no effect on atmospheric temperature.

Each small parcel, let’s say each kilogram, of the atmosphere has a current temperature. This temperature is a reflection of its specific internal energy.[2] Taking a Lagrangian point of view, changes to specific internal energy result from integrated inputs over time of heat added to the parcel through external sources like radiation and internal sources like latent heat or dissipation of kinetic energy, less the work the parcel performed against its environment over its path from a point of origin to the present location.[3] This represents an enormous amount of information. It explains the enthusiasm for the 1-D model, radiative-convective equilibrium (RCE), and the preponderance of feedback analysis based on it.

What about RCE?

Though I find the concept of equilibrium dubious, the transport of heat to space by combined radiation and convection we will call RCE as does Caballero and Merlis. The only place I have ever observed the invariant 6.5 K/km lapse rate, which the simple model of greenhouse warming needs, is among the models in MODTRAN.[4]  MODTRAN is an excellent learning tool for exploring how atmospheric structure affects the transport of thermal IR radiation. It is a reasonable calculator of thermal IR within certain limitations. It can, for example, show that a doubling of CO2 produces the immediate decrease in outgoing longwave radiation (OLR) of 3.7 W/m² at the tropopause, which in turn requires an increase of about 1C in surface temperature to restore OLR to its previous value assuming no water vapor feedback.

The limitation of most concern here is that the implementation available to us does not allow building a custom deck of atmospheric structure. Instead we are limited to using a fixed set of atmospheric models with a few adjustments for clouds. All of these models involve a long segment of temperatures at a fixed, constant lapse rate near 6.5 K/km. Changing the surface temperature of a model, changes the entire vertical column by this same adjustment. Thus, MODTRAN enforces an invariant lapse rate, and one model, the U.S Standard Atmosphere of 1976, presents a constant lapse rate of 6.5 K/km all the way from surface to space. It is the embodiment of the simple model of climate warming under discussion here.

The various models that MODTRAN makes available are all fictions. The U.S Standard Atmosphere of 1976, for example, began as the NACA Standard Atmosphere in 1922. It was not meant as a tool for weather and climate, but to provide input into operational and engineering problems of aeronautics. By the 1950s problems of aeronautics broadened into problems of astronautics. This combined with growing understanding of the upper atmosphere initiated a series of updates starting in 1953 to eventually become the U.S Standard Atmosphere of 1976. I don’t know the precise origin of MODTRAN’s other models, but they all originated apparently out of engineering needs in weaponry and instrumentation; not weather and climate. Nonetheless, mission creep has allowed these to enter weather and climate. As an example,  the U.S Standard Atmosphere of 1976, provides weighting (contribution functions) on the GOES-R baseline imager.[5]

As a consequence of not being able to design a model atmosphere, using MODTRAN as a calculator of greenhouse effect presents an inconsistency. The specified temperature profile can’t be sustained by radiative transport alone as Figure 2a shows. Other mechanisms implicitly fill the gap, and we can hardly imagine how these operate, or how they impact the story of changing CO2, without other information. Figure 2b shows that the temperatures profiles in MODTRAN demand that heat actually be supplied as advection from lower latitudes if, for example, the subarctic winter model is to have real meaning.

Our understanding of feedbacks in RCE, as reference [1] states, really only clearly involves the “R” part and “C” becomes conjecture.

Figure 2a and 2b.

An occasional contributor to threads on WUWT has taken an interesting, and in my view clever,  approach to the “C” part of RCE. I don’t wish to speak for, or identify, this correspondent, but they might volunteer to provide a link to their work, making it visible to readers. In lieu of that, I’ll summarize what I view as pertinent.

Figure 2 implies that radiative transport grows kind-of linearly as the other, unspecified means of transport diminish with altitude. Assuming that the other transport is entirely heat transported vertically from the local surface to space through material motion, a total transport equation from the Schwarzschild equation plus a convective contribution is then written in a parameterized form. A term such as  λ = A∗(1 + Bx), with A and B as constants, represents a characteristic length for radiation absorption/emission – greater by a factor (1+AB)/A at the tropopause (x=1) than at the surface. This λ factor multiplies the Schwarzschild transport terms. A term such as κ = C ∗ (1 − Dx) multiplied by temperature gradient, describes the decline with height of convected (sensible plus latent) heat.[6] The numerical solution is via a variational method.

The approach is not without some limitations. First, it makes no allowance for advected heat.  Second, it uses a linear gradational gray atmosphere model; whereas the real atmosphere differs from this because water vapor is so concentrated near the surface. Third, it makes no explicit allowance for the work done against the surrounding atmosphere in vertical motion, although I suspect that this third shortcoming is mitigated to some extent by choice of C and D. Nevertheless, despite these shortcomings, a couple of pertinent conclusions arise.

First, the 1-D RCE model produces not a constant lapse rate, but one varying systematically from surface to space. As the correspondent says “While lapse rate variations with altitude might seem testable, actual plots appear visually linear and suggest otherwise.”

Second, small perturbations to λ, k, and surface temperature produce sensitivity values lower than what one would surmise by using MODTRAN and the invariable lapse rate as a calculator.

Interesting!

What about Radiative/Advective Equilibrium (RAE)?

Once again we are not necessarily speaking of equilibrium, but rather just heat transport by radiation and advection. The Caballero and Merlis paper’s focus is on this issue.  This paper describes the construction and testing of a very simple model of the north polar heat transfer. The authors say that warming of the poles in response to global forcing is not fully understood and that this

“…motivates interest in developing a minimal model of RAE that robustly captures

the basic physics of high-latitude climate, as a counterpart to single-column RCE for lower latitudes…”

Note, in particular, an implied dichotomy here between an RAE model for polar regions and an RCE model for lower latitudes. I’ll make some comments about this dichotomy later, but for now I will focus on a critique of the content of the paper.

In order to fully model heat transport, one would need a simultaneous solution to several differential equations. The principle one is a statement of the First Law of Thermodynamics. Let’s state this in English rather than mathematics.

We are interested in changes in internal energy of a parcel of air, which comes about through

a summation of 1) radiative transport (Schwarzschild), plus 2) bulk material transport (3-D dot product of material velocity and temperature gradient), plus 3) a diffusion term to smooth the stark temperature gradients (frontal features) that bulk transport alone produces, and finally 4) heat sources and sinks.

There are several challenges to an effort based on this complex set of partial differential equations. First, the least onerous problem is there being a dominating effect on vertical mass transport of the parcel working against the surrounding atmosphere. This suggests that two different but related temperatures are involved; absolute temperature for category 1 and potential temperature for categories 2 and 3.

Second, the more difficult problem is the need for a 3-D velocity. This means that one cannot produce a First Law statement of an RAE model from just a vertical sounding. One requires a reasonable solution over a 3-D domain. This problem is recursive, drawing in progressively larger regions, and soon one is faced with the prospect of a global climate model run innumerable times to fully populate a sort of factorial experiment with results.

What the authors sought instead was a very simple model that captures the essence of energy transport in the Arctic, but which can provide large numbers of simulations with modest resources and good fidelity.

The simple way to accomplish this was to produce a latitude limited model with a single boundary at the arctic/midlatitudes transition, and employing only an energy balance equation. In effect, the Arctic is represented by a single vertical column. The single boundary condition could be made constant in order to perform numerical experiments on internal processes in the Arctic, or manipulated to perform numerical experiments on factors external to the Arctic. The article goes on to establish validity of the model by comparison with reanalysis and global climate model results. Finally conclusions regarding how various forcings and perturbations expected in the future will affect Arctic climate. Those interested in details can consult the open source paper for details.

I am not endorsing the product that resulted. The authors’ goal was to explore Arctic climate change by the usual forcings: change to surface heat, change to CO2 concentration, change to specific humidity, with the advective forcing added as something new. My hope was different. I hoped to see advective heat transfer added as a global feedback in its own right. Mine wasn’t met.

The dichotomy of RAE and RCE based on latitude specific boundaries is not consistent with this hope. Figure 3 shows why.

Figure 3. Heat surpluses/deficits on average over a year on Earth and the implied advective heat transport that a steady climate then requires. [7]

It is obvious that with a surplus of energy input to the tropics and deficit at the poles, RCE alone without advection would lead to increasing tropical temperatures and declining polar temperature. Advection is a global phenomenon, and figuring how it will change with CO2 additions seems pertinent.

My second concern is with limiting analyses to a latitude range, justified by the authors by reference to other work showing …

“…that while the poles respond strongly to forcing applied in lower latitudes, the opposite is not true: midlatitude temperatures are, to a first approximation, unaffected by polar forcing….”

Figure 4 shows a sounding from Dallas-Fort Worth. A Texan I heard once said, “They ain’t nothin’ between Texas and the North Pole, but a barb’ waar fence.” The relevance of this statement to Figure 4 should be obvious. Flows of fluid, air and seawater, into polar regions have to be mass balanced by flows in the opposite direction.  Figure 4 shows the consequence of such a flow. Surface temperature in Figure 4 is -17C and from the dew point values the mixing ratio is less than 0.8g/Kg decreasing upward. Normal values of mixing ratio at this season are two to four times higher. Polar air mass has produced significant effects far south of this putative subarctic/midlatitude boundary.

Figure 4.

The so-called surface radiator fin

Caballero and Merlis identify a significant polar cooling mechanism that they say depends on an atmospheric profile like that in Figure 4. A cold surface with a temperature inversion and dry air above it can radiate freely to space because the atmospheric window of IR thermal radiation is open. The atmosphere can exchange energy through both radiation and diffusion with the nearby surface, and the surface, which approximates a blackbody, then radiates to space efficiently through the window.

Never mind that this isn’t what fins do or how they work[8], this same mechanism or some small variation of it works globally. In fact, even if the temperature inversion is not initially present, the presence of dry air and a wide open atmospheric IR window will produce it. Figure 5 shows a late summer example at Santa Teresa, New Mexico; a locality and situation similar to what I presented in this essay. Overnight there has been a systematic cooling of the air column below 730mb and development of an inversion because of the presence of the radiating ground below – the mixing ratio isn’t even especially dry, being around 10-12 g/Kg near surface.

Figure 5

While Figure 4 showed an unusually severe example of the southward flow, Figure 6 shows that shallow domes of polar air flow during winter deep into the tropics. These not only absorb heat along the way, but because of their relatively dry surface air, they also open the atmospheric window to IR radiation directly to space.[9]

Figure 6. Two instances of mobile polar highs penetrating deep into the tropics. I modified this only slightly from the original by shading land areas to make the paths of travel more clear.

Finally to place these into a clearer heat transport context, Figure 7 shows a numerical simulation of Rayleigh-Benard convection which is the prototype model of natural convection. The lower boundary is heated. The upper boundary cooled.

Note that the fluid motion in this instance involves not a smooth, regular overturning of the fluid, but rather consists of discrete blobs of fluid – red ones rising and blue ones sinking. The appearance of blobs versus smooth overturn is a function of the Rayleigh number which in this example is Ra=10⁸, which is far above the onset of fluid overturn.

In the context of the midlatitudes atmosphere, the blue blobs are mobile polar highs gliding equatorward along the Earth’s surface. The red blobs are the warm counterflow of air/moisture travelling poleward in slant convection or some other mechanism that lofts and bulldozes air to higher latitudes. The mobile polar highs take relatively cool air that can absorb some heat and moisture in the midlatitudes and even into the tropics, but more importantly they take with them dry surface air that presents an open IR window in places where one doesn’t otherwise exist.

Figure 7. Numerical simulation of Rayleigh Benard convection. Image from Lappa, Marcello. (2019). On the Nature of Fluid-dynamics. Uploaded to Researchgate by Marcello Lappa.

Conclusions

The effort of Caballero and Merlis, which initiated this essay, failed to produce what I had hoped primarily because their goal was, as usual, demonstrating how CO2 can make the polar regions warmer. Because of this they stopped short of a worthy goal. That goal is to quantify how the resulting warmer polar regions will take heat from the surface to space because a warmer surface radiates more heat via the Stefan-Boltzmann feedback and does so in the driest portions of the atmosphere with a wider atmospheric window.

Advection not only moves heat over the Earth’s surface to where it can travel more easily from surface to space, but the very dry air in the counterflow of cA and cP masses that polar regions produce open the atmospheric window to space along journeys to warmer regions. Global advection deserves more attention than it has received to date.

References and Notes

1-Caballero and Merlis, Polar Feedbacks in Clear-Sky Radiative–Advective Equilibrium from an Airmass Transformation Perspective, Journal of Climate, V 38, p. 3399, 15 JULY 2025

This paper begins thusly, which was my motivation for this current essay.

“The concept of radiative–convective equilibrium (RCE) and its embodiment in a single-column model (Manabe and Strickler 1964; Manabe and Wetherald 1967) are the foundation of our understanding and quantification of climate sensitivity.”

2-internal energy equals heat capacity at constant volume times temperature plus some arbitrary reference value. Heat capacity is a function of temperature as more degrees of freedom become available at higher temperature, thus more ways a molecule has to store energy.

3-focussing on the parcel of atmosphere as our thermodynamic system, the sign convention of mechanical engineering is that heat added to the parcel is positive (thus heat subtracted is negative), while work the parcel does on its environment is positive. Writing the First Law of Thermodynamics as an equation in small quantities; δU =  δQ –  δW; where U is internal energy. Physicists and chemists more generally reverse the sign convention for work.

4-The version I use is available at University of Chicago. I know of only one other version which seems to have all the same limitations.

5-Timothy J. Schmit, et al, 2017, A Closer Look at the ABI on the GOES-R Series, Bulletin of the American Meteorological Society, 01 Apr 2017, p. 681-698.

DOI: https://doi.org/10.1175/BAMS-D-15-00230.1

6-Heat transport by moving fluid is always represented mathematically by a term something like a dot product (vector inner product) between the vectors of fluid velocity and temperature gradient. Thus, the convection as a parameterized velocity (k term) and vertical temperature gradient is appropriate in this 1-d RCE formulation. However, the presence of positive work output of a parcel as it rises suggests that potential temperature is more appropriate.

In a 3-d model the horizontal advection of heat at any height would involve a term like V·∇T; where V is the horizontal velocity vector, ∇ is the horizontal gradient operator (Grad of div, grad, curl fame) and the middle dot represents the horizontal dot-product. The vertical component typically uses omega as the velocity unit.

7-Adam Showman, J. Y-K. Cho, Kristen Menou, 2009, Atmospheric Circulation of Exoplanets, https://www.researchgate.net/publication/45884771; see for example equations 5a through 5e. Note that 5e has the advective/convective terms separated with the convective term written in terms of omega (vertical velocity in pressure coordinates). Omega is much smaller than the horizontal components, and to try to find it through observations by using 5c renders it mostly in  error.

8-”Radiating fins” work simply by providing a low conductance path for heat into a broad region where the heat can be disposed of by fluid convection. The typical fin geometry makes a poor true emitter of radiation because each fin has a large view of others at the same temperature.

9-Leroux, M, 1993, The Mobile Polar High a new concept explaining present mechanisms of meridional air-mass and energy exchanges and global propagation of palaeoclimatic changes, Global Planet Change, 7 69-93

Related