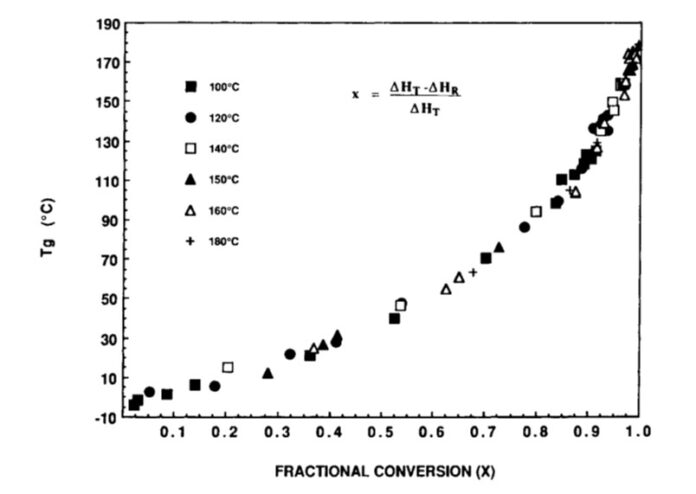
This post will further explore multiple studies that have demonstrated the universal nature of the Tg-conversion relationship. The seminal paper by Professor John Gillham and his Ph.D. students was published in 1990 that very clearly articulated the concept of how the fractional conversion impacts the glass transition temperature during curing as shown in Figure 1.
Figure 1. Tg is plotted as a function of fractional conversion from reference [1].
Additionally, as discussed in the last post, the Tg-conversion relationships were also demonstrated during isothermal and non-isothermal curing for an epoxy resin cured with an imidazole hardener [2]. A plot of Tg-fractional conversion is shown in Figure 2.
Figure 2. Glass transition temperature (Tg) as a function of percent conversion for non-isothermal (heating rates noted in the legend) and isothermal curing profiles [2].
The data in Figure 2 falls on a single curve. The significance of this is that the curing is “cure path independent” meaning the Tg – conversion relationship will be the same for either isothermal or non-isothermal curing. The solid line in Figure 2 is the DiBenedetto equation which will be discussed later in this post.
In the same timeframe, Dr. Sue Ann Bidstrup and colleagues at MIT were investigating the use of dielectric spectroscopy to monitor the curing of epoxy resins [3]. They studied the curing of a standard epoxy resin (DGEBA) cured with diamino diphenyl sulphone (DDS) a common hardener used in high temperature epoxy systems. Their work correlated the Tg with the dielectric properties during curing, but they also determined the relationship between Tg and conversion as shown in Figure 3.
Figure 3. Tg versus conversion for an epoxy resin (DGEBA) cured with a DDS hardener [3]. The solid curve represents the DiBenedetto equation.
The DiBenedetto equation provides a means to correlate Tg with conversion (α) [4-6]:
Where:
Ex/Em is the ratio of lattice energies for crosslinked and uncrosslinked polymer
Fx/Fm is the ratio of segmental mobilities in the crosslinked and uncrosslinked polymers
Tgo is the Tg of the unreacted material (i.e., no cure)
In the work of Bidstrup et. al., Tgo was measured to be 5°C
In Figure 3, the values of Ex/Em = 0.39 and Fx/Fm = 0.24 were determined using curve fitting methods [3].
Further work by Wisanrakkit and Gillham [7] showed that the Tg obtained using Torsion Braid Analysis (TBA) could also be correlated with conversion. The fractional conversion was measured on the TBA samples using DSC. Figure 4 shows the TBA Tg – conversion relationship and the fit to the DiBenedetto equation for an epoxy (DER 332) and a diamine (TMAB) [7].
Figure 4. Tg measured using TBA versus DSC fractional conversion at various isothermal temperatures. The DiBenedetto equation is shown as the solid line [7].
In conclusion, several researchers using different epoxy systems have found a consistent relationship between the Tg and the fractional conversion. There are important practical implications for the relationships shown in Figures 1-4. During processing it is critically important to drive the process to achieve high degree of conversion since we have seen a very large increase in Tg over the final 10 percent of fractional conversion. When investigating the curing of a thermosetting polymer system, one of the first tasks should be to determine the ultimate glass transition temperature which is denoted at Tg∞.
References:
- Wisanrakkit, G. and Gillham, J. K., Journal of Applied. Polymer Science, 41, 2885 (1990).
- Fuller, J. Gotro, and G. Martin, “Analysis of the Glass Transition Temperature, Conversion, and Viscosity during Epoxy Resin Curing,” Advances in Chemistry Series, No. 227, in Polymer Characterization: Physical Property, Spectroscopic, and Chromatographic Methods, Clara Craver and Theodore Provder, Editors, page 215, 1990, American Chemical Society.
- A. Bistrup, N.F. Sheppard, and S. D. Senturia, Polym. End. and Sci., Mid-March, Vol 29, No. 5 (1989)
- T. DiBeedetto and L. E. Nielsen, J. Macromol. Scil, Rev. Macromol. Chem., C3, 69 (1969)
- E. Adabbo and R. J. J. Williams, J. Appl. Polym. Sci., 27, 127 (1982)
- B. Enns and J.K. Gillham, J. Appl. Polym. Sci., 28, 2567 (1983)
- Wisanrakkit and J. Gillham, J. Journal of Applied. Polymer Science, 42, 2453 (1991).