Moving, But Not In A Straight Line – Watts Up With That?

Guest Post by Willis Eschenbach.

I must confess, I use WUWT as a lab notebook on steroids. It reflects my latest work, my latest calculations, my latest graphics, my latest theories. My thanks to all participants who make this possible: Anthony Watts, Charles The Moderator, anonymous moderators around the planet, as well as all the commentators and lurkers who keep me from going off the rails and suggest new avenues to explore. What a time to be alive!

Onwards. Here’s my latest.

I was watching a National Geographic documentary about the use of airborne lidar to look straight down and see through the trees of the Guatemalan jungle to expose Mayan ruins. The commenter said “If we see straight lines on the ground, it’s not natural. It’s something made by man.”

And it’s true—in general, nature doesn’t do straight lines. As the poet said:

“Glory be to God for dappled things –
        For skies of couple-colour as a brinded cow;
 For rose-moles all in stipple upon trout that swim;
        Fresh-firecoal chestnut-falls; finches’ wings;”

I’m reminded of this by what I see as a ludicrous claim—that regarding the climate, one of the more complex systems we’ve ever tried to analyze and understand, mainstream climate scientists say that there is a straight-line linear relationship between changes in the radiation balance at the top of the atmosphere and the surface temperature. This is a central belief in their understanding of the climate:

∆T =  λ * ∆F                                       (Equation 1 And Only)

This says that the change (delta, “∆“) in global average surface temperature (“T“) is equal to the change (∆) in “forcing” (“F“) times a constant called lambda (“λ“) that is known as the “equilibrium climate sensitivity” (ECS).

And what is forcing when it’s at home? Forcing is a term of art in climate science. Radiative forcing is defined by the Intergovernmental Panel on Climate Change (IPCC) as:

“The change in the net, downward minus upward, radiative flux (expressed in W/m²) due to a change in an external driver of climate change, such as a change in the concentration of carbon dioxide (CO₂), the concentration of volcanic aerosols, or the output of the Sun.”

The “downward” radiation at the top of the atmosphere (TOA) is the incoming sunshine. It’s all the radiation entering the system.

The “upward” radiation is the longwave thermal radiation heading to space. It’s the total of all the energy leaving the system.

Now, that claim of linearity makes absolutely no sense to me. Let me explain why.

First, the surface temperature can change without affecting the TOA radiation balance. The climate system is a giant heat engine. Heat comes in at the hot end of any heat engine: in this case it’s the tropics. Then it does work with some of the heat, and the rest of the heat is exhausted at the cold end of the heat engine: in this case, the poles.

Note that only part of this heat is converted into work. The rest is just passing through, carried by the ocean and the atmosphere from the tropics to the poles and back out to space. Any variation in the percentage of the total flow which is converted to work will change the surface temperature without any change in the TOA radiation balance.

Next, the climate system isn’t free to adopt any configuration. It is ruled by the Constructal Law, and like a river meandering to the sea, it doesn’t move in straight lines. Like all flow systems far from equilibrium, the river is maximizing flow, and thus the river picks the longest possible path to the sea.

Similaryly, as a constructally ruled system, the climate is always seeking to maximize the flow from the tropics to the poles. And as that flow speed changes, the surface temperature changes … without any corresponding linear change in the TOA radiation balance.

Finally, their Equation 1 equates a quantity that IS conserved (watts per square meter) with a quantity which is NOT conserved (temperature). I’m not clear how that is even possible.

However, for the purpose of this discussion, let’s assume that they are right about that particular relationship between TOA forcing and temperature. We’ll follow that path and see where it leads.

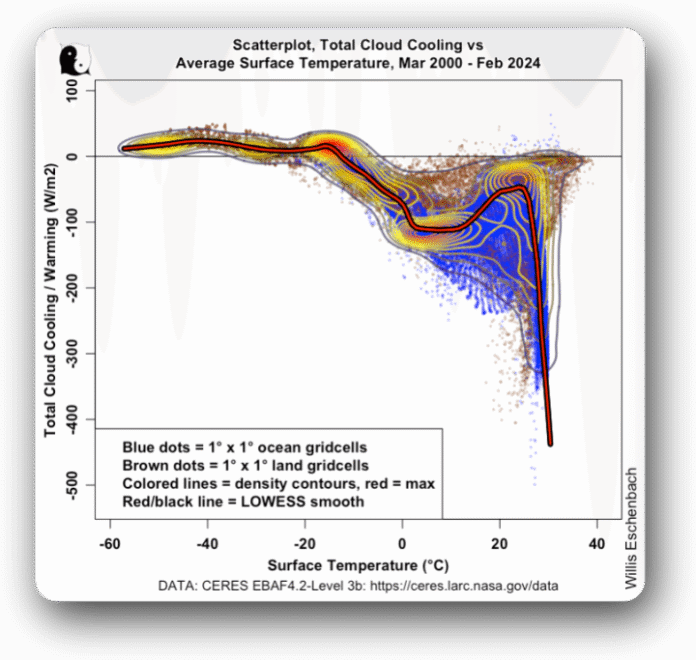
As a first step along that path, let me return to the idea that the climate doesn’t move in straight lines. For example, below is a graph of gridcell-by-gridcell total cloud cooling/warming, which is a combination of the clouds’ effects on longwave and shortwave radiation plus the evaporative cooling related to rainfall. I’ve compared it to gridcell surface temperatures in a scatterplot with contour lines.

Now, I started doing these scatterplots like in Figure 1 below, comparing two variables for every 1° latitude by 1° longitude gridcell of the planet, for a simple reason. They show the long-term relationship between the two variables. Each gridcell on the planet is in a long-term, general steady state regarding the various measurable factors, like say thunderstorm prevalence. Annual averages of these relationships vary little, and a 24-year average reveals the underlying long-term relationship of the variables.

And this lets us investigate things like the long-term value of the equilibrium climate sensitivity … but I get ahead of myself …

Figure 1. Scatterplot plus density contour lines and LOWESS smooth. Total cloud cooling versus surface temperature, entire planet.

Back to figure 1, there’s much of interest. First, in gridcells with average temperatures below about -20°C, which is Greenland and Antarctica, the clouds warm the surface. Then when the frozen ocean comes into play, from -20°C  to where the gridcells average about freezing, there is cooling increasing with temperature.

Then the trend reverses, and cooling decreases with temperature up to the gridcells with an average temperature of 25°C or so. And above that, the cooling increases radically and almost vertically to the point where it is cooling those gridcells by -400 W/m2 or so.

In passing, note the peak around 25°C. If the temperature goes above that, the clouds increase their cooling, eventually to a radical extent. And when the temperature goes below ~ 25°C, the clouds decrease the amount of cooling. This is clear evidence of the thermoregulatory action of clouds, cooling more when it’s warmer and less when it’s cooler.

Finally, the predominant role of the ocean is evident in both the tighter grouping and the larger number of the blue oceanic dots compared to the brown dots showing land gridcells.

And to close the circle, the red/black line showing the change of cooling with temperature is kinda the definition of non-linear …

Now, these kinds of graphs are very useful for a simple reason. The slope of the red/black line at any point gives the average change in the y-axis variable for a 1°C change in the surface temperature. So for example, we can see that when it’s above say 25°C, the total cloud cooling increases extremely rapidly with each 1°C increase in temperature.

With all of that in mind, what can such graphs show us about the long-term relationship between temperature and forcing?

The mainstream theory goes like this: 

• Doubling the amount of CO2 intercepts more of the upwelling longwave radiation headed to space.
• This leads to a top-of-atmosphere (TOA) radiative imbalance. 
• The Earth then warms up until the balance is restored.

So the question becomes … how much does the earth have to warm up to restore the 3.7 watts per square meter (W/m2) of TOA radiation imbalance that is said to result from a doubling of CO2 (2xCO2)? 

This amount of warming required to rebalance the TOA radiation imbalance is called the “equilibrium climate sensitivity” (ECS) to a doubling of CO2. It’s the “lambda” in the linear Equation 1 (and only) above.

To investigate the value of the ECS, here is the scatterplot of the TOA imbalance versus the surface temperature.

Figure 2. Scatterplot plus density contour lines and LOWESS smooth. Top of atmosphere radiative imbalance versus surface temperature, entire planet. The percentage (% area) numbers show the percentage of the surface area in each temperature interval.

Man, I love being surprised by my investigations. It’s the best part of my scientific education. I definitely did not expect the graph to look like that. But facts are facts. 

At temperatures below -20°C, the brown dots show it’s just land— Greenland and Antarctica. And there, curiously, the TOA imbalance gets more negative for each 1°C of warming. Then, at around -15°C, the slope reverses as the frozen ocean comes into play. It increases, somewhat linearly, until about 20°C or so, after which the imbalance starts increasing at a faster rate.

We can visualize these changes in detail by calculating the slope at each point in the red/black line. Recall that the slope is the change in TOA radiation imbalance per degree of warming. Here is that result.

Figure 3. Slope of the red/black trend line shown in Figure 2 above. If you wonder why the area-averaged change is so high, look at the percentages of the global area with annual average temperatures in each temperature interval.

I’ve included the area-weighted average of the change in the TOA balance from a 1° increase in surface temperature. It’s 6.6 W/m2 per °C. This implies an equilibrium sensitivity (ECS) of 0.6°C per doubling of CO2

I’m gonna say that is a reasonable estimate for the ECS, for a couple of reasons.

First, this ECS estimate of 0.6°C is not outside the range of other observational estimates of CO2 sensitivity. In the Knutti dataset there are the results of 172 people’s calculations of the ECS, using different methods. My estimate is at the low end, but it isn’t the lowest.

Figure 5. Estimates of ECS from theory and reviews, observations, paleoclimate studies, climatology, and climate models. Note that in the last half century these estimates have grown more scattered, not less. And it’s particularly true for climate models (yellow dots).

The second reason I think that my ECS estimate of 0.6°C per 2xCO2 is valid is that it agrees with what I said about my previous estimate of the ECS, which was based on my implementation of Bejan’s Constructal climate model. The model is described in the post below.