Temperature – a driver of the carbon cycle – Watts Up With That?

From Climate Etc.

By Joachim Dengler

Are the natural carbon sinks failing?

For a long time, the discussion about the relation between temperature and CO₂ concentration has been focused on the greenhouse effect and its possible feedback mechanisms, captured by the concept of sensitivity.

Here, I would like to shift the focus to the other side of the story: the possible causal influence of global sea surface temperature on the growth of CO₂ concentration. Some readers may see this as a contradictory paradigm to the greenhouse effect; others may see it as one of the feedback mechanisms of the greenhouse effect.

The motivation for the investigations constituting the background paper of this post, “Evaluating the Effectiveness of Natural Carbon Sinks Through a Temperature-Dependent Model”, was published in the mainstream media like the Guardian, claiming that “Trees and land absorbed almost no CO₂ last year. Is nature’s carbon sink failing?“. A closer examination of all the articles published on this topic revealed that they all refer to a single publication. The scientific basis and trigger for the discussion had been a preprint of this article: “Low latency carbon budget analysis reveals a large decline of the land carbon sink in 2023”.

To find an appropriate answer to this, it is necessary to take a closer look and use original data to examine how the changes in CO2 concentration develop. In a scientific paper, it is legitimate to state, even guess, a model of a given form and relate this to measurements. This is what I did in the background paper by setting up a sink model that depends on both CO₂concentration and temperature. I underestimated the consequences of decades of debates about the relationship between CO₂ concentration change and temperature change. Before evaluating the interesting implications of the temperature-dependent model, I found myself confronted with fundamental doubts and prejudices. Therefore, I deviate from the structure of the published paper and begin with a visual introduction to the subject.

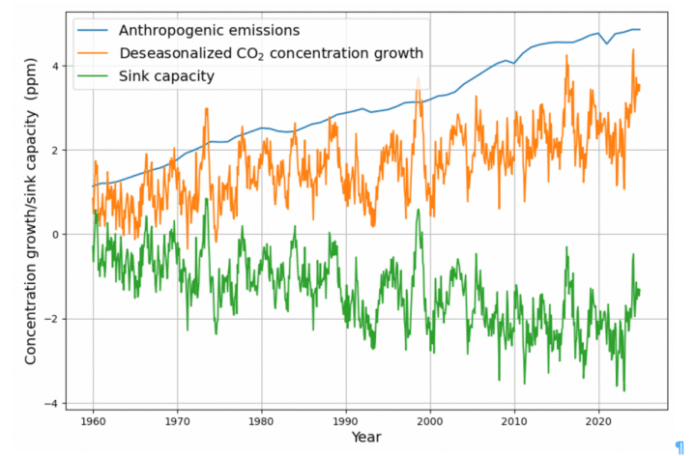
The effective monthly CO2 sink capacity is measured as the difference between the monthly anthropogenic emissions and the growth in concentration:
<sink capacity> = <anthropogenic emissions> – <concentration growth>     (1)
To measure concentration growth independently of seasons, growth is defined as the difference between the current concentration and the concentration 12 months prior.

Figure 1: Anthropogenic emissions (blue), CO₂ concentration growth (orange), and sink capacity (green). The Sink effect has a negative sign (for display purposes only).

From the continuity equation, it follows that the sink capacity is also the difference between global absorptions and natural emissions:
<sink capacity> = <global absorptions> – <natural emissions>            (2)

Anthropogenic emissions, concentration growth, and sink capacity are displayed in Figure 1.

Motivating the temperature-dependent model with Henry’s Law

Henry’s law describes the exchange of gases, here CO₂, between a liquid, where the gas is dissolved, and the gas phase, here in the atmosphere. In the equilibrium, the concentration  C  of the dissolved CO₂ is related to the partial pressure P of CO₂ in the atmosphere by C = k^.P, where k is Henry’s law constant (mol/(L·atm), specific to CO₂ and temperature, C is measured in mol/L, and P is measured in atm. The numeric value of the partial pressure P corresponds to the CO₂ concentration, measured in ppm, because the total atmospheric pressure is assumed to be 1 atm.

Henry’s law constant k is influenced by temperature, salinity, and pH. Given the actual measured conditions of the Earth’s oceans, temperature is the dominant factor influencing k and thus CO₂ solubility. Its large spatial variability (0–30°C) drives significant regional differences in air-sea CO₂ flux, with cold polar waters acting as CO₂ sinks (higher solubility) and warm tropical waters often acting as sources (lower solubility). For example, the solubility of CO₂ in polar waters can be more than double that in tropical waters due to temperature alone. The temperature dependence of the solubility on k is displayed in Figure 2. Despite the complex, nonlinear mathematical form, the temperature dependence of solubility is close to antilinear, getting smaller with growing temperature.

Figure 2: Temperature dependence of Henry’s law constant (solubility).

The downwelling flux of CO₂, the sink effect, is proportional to the difference between the equilibrium concentration k^.P  and the actual concentration C of the dissolved CO₂.
Without diving here into the details of the computation, this suggests that the ocean sink effect not only depends on the CO₂concentration via the partial pressure P, but also on temperature, which dominantly determines Henry’s law constant k.
This is visualized in Figure 3, taken from the publication “Uptake and Storage of Carbon Dioxide in the Ocean: The Global C02 Survey“

Figure 3: Ocean net CO2 flux map.

Although the authors state that rising emissions due to higher temperatures are compensated by reduced dissolved CO₂ concentration from increased biological activity of phytoplankton, the map indicates that areas of net absorption are near the poles, and regions of net emissions are near the equator. The map clearly shows that higher temperature implies higher emissions, respectively, lower absorption. Phytoplankton therefore reduces the temperature-dependent increase of natural emissions, but it does not fully compensate for it.

Similarly, the decay of biological matter and organisms is related to van’t Hoff’s rule, which states that an increase in decay rate and, thus, natural emissions scale with an increase in temperature. Of course, the sustainable availability of decayable substances depends on photosynthesis. Photosynthesis also scales with sunlight hours and temperature up to 30 °C, besides scaling with CO₂ concentration. CO₂ fertilization dominates the greening of the Earth, which has been more than 30% since 1900. So, it is logical that absorption dominantly scales with CO₂ concentration, while biological decay, implying natural emissions, scales with temperature. When both are correlated as they have been for the last 65 years, a balanced growth of both is expected.

The temperature-dependent model

We recognize from Figure 1 that CO₂ concentration can change very fast. Therefore, the input data are monthly time series of CO₂concentration and sea surface temperature.

Because it takes time to heat the ocean in summer and cool it down in winter, we allow several months of time lag between sea surface temperature changes and subsequent sink changes.

The simplest sink model with the dependency on CO₂ concentration and temperature is a linear model
<sink capacity> =     a^.<concentration> + b^.<temperature> + c      (3)

This model has been presented before; new insights are gained by changing the data granularity to months and optimizing the time lags between concentration growth and temperature.   Independence from seasonality and noise reduction is reached by averaging the measured data over 12 consecutive months. Nevertheless, the time lag is computed with a monthly resolution.

When estimating the optimal parameters a,b,c of equation (3) for a measured sink capacity according to equation (1), the explained variance (R² value) depends on the time shift between the temperature measurement and the subsequent CO₂ sink capacity.  This is displayed in Figure 4.  With a 4-month time lag, the model explains 80% of the data variance, compared to 57% when a sink model without temperature dependence is applied, i.e., when b=0.

Figure 4: Explained variance of the concentration and temperature-dependent sink model

This is reflected in the quality of approximation of the measured smoothed sink capacity, as displayed in Figure 5. While the concentration-based simple model explains the trend, the new model, including temperature, also explains most of the short-term variations.

Figure 5: Measured sink capacity (blue), approximation with simple sink model (green, only CO2 concentration), and temperature-dependent model (orange).

There is only one significant outlier. The sink capacity between 1991 and 1994 is considerably larger than predicted by the model. Roy Spencer explained this as a consequence of the Pinatubo eruption in 1991, where the dust-induced increased diffuse light increased photosynthesis considerably.  Otherwise, the predicted value of the actual concentration growth is remarkable, as shown in Figure 6. Again, for comparison, the prediction of the simple sink model without the temperature term is shown as the green graph. The fact that the green graph clearly shows a consistent declining trend since 2013 indicates that the concentration-dependent causes for sink capacity are more likely to have increased instead of decreased.   The details of the concentration growth are remarkably well predicted by the sea surface temperature. In particular, the sharp rise in concentration growth since 2023 is entirely temperature-based.

Figure 6: Monthly concentration growth (blue), modelled with concentration only (green) and additionally with temperature (orange).

Intuitive understanding of model parameters

Looking at the graphs, the introduction of temperature dependence seems to influence only short-term data variability. But temperature has a trend. This has severe consequences on the resulting parameters, shown in Table 1.

Table 1: Regression results of simple and extended sink model

In the simple, temperature-independent model, the absorption is only about 2% of the concentration, whereas the temperature-dependent model implies 5%. This is a severe discrepancy that deserves attention.  The mathematical explanation of the discrepancy can be found in section 5 of the 2024 publication.  If, in reality, sink capacity depends on temperature and temperature is strongly correlated with CO₂ concentration (which is the case), if you then offer a mathematical model that contains only CO₂ concentration as a parameter, then the CO₂ parameter will also take the role of the missing temperature.

Figure 7 conveys an intuitive understanding by assuming that down-welling absorptions are controlled by CO₂ concentration (green arrow), while natural emissions are controlled by temperature (blue arrow). By definition, their difference is the measurable sink effect (red arrow). When temperature is essentially a linear function of CO₂ concentration (which is the case since 70 years), then in the long term, the concentration trend cancels the temperature trend. In the sink capacity, therefore, only the short-term variability of temperature is visible.

Figure 7: Intuitive explanation of apparent model discrepancy.

Validating the model with ¹⁴C decay after the bomb test ban treaty

The nuclear bomb tests beginning in the 1950s stopped rather suddenly in 1963 with the Nuclear Test Ban Treaty. This provides a close-to-ideal identifiable carbon emission pulse of ¹⁴C that has been thoroughly investigated for more than 40 years. The data series is the global data sequence from 1950 to 2019 from the supplements of the article “Atmospheric Radiocarbon for the Period 1950–2019“. The relative deviation from the preindustrial zero level of ¹⁴C concentration, Δ¹⁴C, is displayed as the blue graph in Figure 8.

Figure 8: Relative deviation from preindustrial ¹⁴C level (blue), adjusted relative deviation of ¹⁴C level by setting pre-1963 level to 0 (orange).

Why is this concentration decay representing “pure” absorptions? The CO₂ emissions from the oceans have the much lower ¹⁴C concentration of the long-term equilibrium before the bomb tests; therefore, the upwelling ¹⁴C can be neglected.
This decay includes both the decay of ¹⁴C concentration into the long-term sinks, but also the Suess effect due to the atmospheric concentration change of ¹²C by anthropogenic emissions. For the determination of the Suess effect, the 25-year interval from 1965 to 1990 with a good ¹⁴C decay signal was taken. The upper bound of the diluting Suess effect due to fossil fuels is obtained by pretending there is no sink effect, thus adding the cumulative emissions of 60 ppm (=127 GtC) between 1965 and 1990 to the 1965 CO₂ concentration of 320 ppm.  This results in a Suess effect contribution of 0.69% per year to the decline of the relative ¹⁴C concentration. With a value of 0.058 for the decay constant of the uncorrected data, the reduction by 0.0069 results in 0.051, the actual absorption constant of ¹⁴C. Considering the 95% confidence interval [0.047,0.055], this is a perfect confirmation of the concentration-dependent absorption constant of the extended sink model.

Validating the model with soil respiration

Photosynthesis is the primary driver of the following processes of plant decay and soil respiration. Net Primary Production (NPP) during the time interval from 1982 to 1999 was investigated. They found a yearly increase of 3.4 GtC of NPP over 18 years. During this time, the temperature increased by 0.25 °C. This would imply a 13.6 GtC increase of bound carbon per °C and year. According to the article, this was not only due to the increase of CO₂ fertilization but also, to a large degree, to the reduction of cloud cover over the Amazon rainforest and an increase in solar radiation, which directly influences photosynthetic processes more than CO2 concentration and temperature. A later reported decline of yearly NPP by 0.55 GtC in the years 2000–2009 adjusts this exorbitantly high yearly number to 2.85 GtC/0.5 °C = 5.7 GtC/°C.

During the 19 years from 1989 to 2008, the natural emissions from soil respiration 𝑅𝑆 have risen by 0.1 GtC per year, i.e., 1.9 GtC during the whole investigation period. During this time, the global temperature has increased by 0.3 °C. Therefore, we have a soil respiration temperature dependency of 6.33GtC/°C. The temperature coefficient of the extended model, is 3.6 ppm/°C = 7.7 GtC/°C with the 95% confidence interval [5.9, 9.5] GtC/°C. This can be considered a sufficiently good match with the evidence from soil respiration.

Other Approaches relating Temperature to Sink Effect

I am aware of two other approaches to deal with the temperature dependence of the sink effect. Both have in common that they do not use temperature itself as a predictor, but a variable derived from temperature, which does not have a long-term trend.  The obvious reason for this approach is the known fact that the measurable sink effect does not show any long-term trend.  As I discussed above, this is a superficial conclusion from the observations; it ignores the fact that due to the large correlation between concentration and temperature, actual temperature effects might be hidden.

Ferdinand Engelbeen has suggested that the sink effect and, as a consequence, the concentration growth, should depend on the time derivative of temperature instead of temperature itself. Indeed, the derivative of temperature does not have a trend.  And the numerical explanation value of the data variance is also 0.8 for his model, the same as for the model described here. Nevertheless, I do not consider taking the derivative of temperature as a predictor for the sink capacity or concentration growth, respectively, a good idea.

Both mentioned natural laws, Henry’s law and van’t Hoff’s rule,  relate natural emissions to temperature and not to its derivative. Also, a simple thought experiment rules out the derivative: Let us assume a single temperature jump of 1 °C at the sea surface, then the temperature is assumed to remain at the elevated level for a long time. If the temperature effect depended on the time derivative of temperature, there would only be a single pulse of natural emissions during the very first time interval. But in reality, temperature is a thermodynamic state variable. This implies increased natural emissions at all times following the temperature step (under ceteris paribus conditions).

Roy Spencer has related the short-term variability of the sink effect to the Multivariate ENSO index (MEI).  MEI is also a trend-free variable, where two of the five components of the MEI are regional sea surface temperature and regional air temperature anomalies. The anomalies are determined by subtracting the 30-year average from the temperature. This removes the trend from the temperature, but preserves the short-term variability.

To understand the relation of these approaches to the temperature-dependent model described here, temperature is decomposed into a linear function of CO₂ concentration, containing the temperature, and a residual temperature. This is displayed in Figure 9.

Figure 9: Monthly sea surface temperature (blue), temperature from linear model of CO₂-concentration (orange), residual temperature (green)

The residual temperature is a residual of a regression model and, therefore, by definition, zero-mean and trend-free. When the residual temperature replaces temperature in the extended model, the results for absorption coefficient a and the constant c are identical to those of the simple model (without temperature), the temperature coefficient b is identical to that of the temperature-dependent model (see details in previous publication). The model reconstruction of the concentration growth is identical to that of the temperature-dependent model.

Comparing the residual temperature with the Multivariate ENSO Index (MEI) and the derivative of the temperature, it becomes clear why all three lead to similar results. All three time series are displayed in Figure 10, slightly smoothed to keep them visually identifiable.

Figure 10 Comparison of Residual Temperature (blue) with the Multivariate ENSO Index (orange) and the Derivative of Sea Surface Temperature (green)

The residual temperature has structural similarities with the MEI signal. When sea surface temperature is indeed a physical driving force of the sink effect and CO₂ concentration growth, it can be expected that MEI has a significant influence on the sink effect. In that case,  I expect that the model based explicitly on sea surface temperature explains the observed data better than the model with the complex MEI index. I invite Roy Spencer and others to determine the R² value when MEI is used besides CO₂ concentration as a predictor.  The first temperature derivative is also quite similar to the residual temperature, but appears time-shifted. This is because the derivative of a periodic function is a phase-shifted version of that function.  Empirically, this is reflected in the fact that the optimal fit requires the derivative of the temperature to be shifted by 9 months instead of 4 months as with the residual temperature.   In contrast, the peaks of the MEI signal coincide with those of the residual temperature; both are essentially the difference between the temperature and its temporally smoothed version.

My reason to prefer the model with the actual temperature is physics.  The elementary sink processes only experience the state variable temperature, not complex derivations of it.

Conclusions

The continuity equation, together with the observed consistent decrease in the ¹⁴C concentration in the atmosphere after 1963 and the observation of temperature-dependent natural emissions, are powerful tools for evaluating observations.

One purpose of this article is to explain the recent rise in concentration growth as a consequence of rising sea surface temperatures instead of a hypothetical unobserved decline in absorption by oceans or plants. While the rise in concentration growth is real, the cause is not a failure of sinks but a larger rise in temperature beyond the trend that corresponds to the CO₂ level rise.

It should, therefore, not be off-limits to consider temperature as a “normal” cause of CO₂ concentration changes in the public debate, as an influencing factor instead of speculating about the absence of sinks without evidence.

This does not exclude causality in the other direction; the greenhouse effect, the rather large temperature coefficient on natural CO₂ emissions, certainly limits the possible climate sensitivity.

The temperature-dependent model makes it possible to better separate the actual anthropogenic origin of CO₂ changes and the natural causes, among which temperature is a very important one. Many people were confused when, in 2020, no effect of the anthropogenic emission reduction could be seen in the concentration growth. When the temperature effect is removed, as is the case in the simple model, then the effect of the lockdown-caused emission reduction can be seen, e.g., the green curve in Figure 6.

The most important contribution is that it became possible to separate downwelling absorptions from upwelling natural emissions. Through the evaluation of the bomb test ¹⁴C time series and by the Suess effect correction, we have a reliable estimate of the yearly absorption rate of 5% of the CO₂ concentration. Together with the precise CO₂ concentration measurements on Mauna Loa and the accepted measurements of anthropogenic emissions from the International Energy Agency (IEA), the continuity equation constrains the yearly net natural emissions. Together with the extended model, we also have an understanding of their temperature dependency.

Related